5 L15: Undetermined Coefficients II (5.5)

5.1 Overview

Method review
Example when the Force is sinusoidal
Real examples: washboard and wake-up strips

5.2 Method of Undet. Coefficients II

\[y''+py'+qy=F(x),\qquad p,q\in \mathbb{R} \tag{5.1}\]

Find \(y_c=c_1y_1+c_2y_2\)
Find \(y_q=c_1y_1+c_2y_2+c_3y_3+\cdots + c_ny_n\)
Find \(y_p=c_3y_3+\cdots + c_ny_n\) by solving for \(c_3,\cdots,c_n\).
Solution: \[ y=c_1y_1+c_2y_2+y_p\]

5.3 Example

\[y''-2y'+y=5\cos 2x + 10\sin 2x\]

Solution:

STEP 1:

Roots of characteristic equation:

\[r^2-2r+1=0\Rightarrow (r-1)(r-1)=0\Rightarrow r=1,1\] \[\boxed{y_c=c_1e^x+c_2xe^x}\] STEP 2:

Roots corresponding to \(F(x)=5\cos 2x+10\sin 2x\):

\[r=\pm 2i\] All roots:

\[r=1,1,\pm 2i\] \[\boxed{y_q=c_1e^x+c_2xe^x+c_3\cos(2x)+c_4\sin(2x)}\]

STEP 3:

\[y_p=y_q-y_c\]

\[y_p=c_3\cos(2x)+c_4\sin(2x)\] \[y_p'=-2c_3\sin(2x)+2c_4\cos(2x)\] \[y_p''=-4c_3\cos(2x)+-4c_4\sin(2x)\] which is a solution of: \[y_p''-2y_p'+y_p=5\cos 2x + 10\sin 2x\] \[\begin{align} -4c_3\cos(2x)+-4c_4\sin(2x)&+\\ -2(-2c_3\sin(2x)+2c_4\cos(2x))&+\\ c_3\cos(2x)+c_4\sin(2x)&=\\ &=5\cos 2x + 10\sin 2x \end{align}\]

Then I can set my system of equations:

\[\begin{align} -4c_3-4c_4+c_3&=5\\ -4c_4+4c_3+c_4&=10 \end{align}\]

Then:

\[\begin{align} -3c_3-4c_4&=5\\ 4c_3-3c_4&=10 \end{align}\]

\[4*eq1+3*eq2=-16c_4-9c_4=50\Rightarrow \boxed{c_4=-2}\] \[-3c_3-4\cdot(-2)=5\Rightarrow -3c_3=-3\Rightarrow \boxed{c_3=1}\]

Then:

\[\boxed{y_p=\cos 2x-2\sin 2x}\] STEP 4:

Finally:

\[\boxed{\boxed{y=c_1e^x+c_2xe^x+\cos 2x-2\sin 2x}}\]

5.4 Vibrations in Damped Oscillators with forcing functions

Forced Damped oscillators formula:

\[y''+2dy'+w_0^2y=g(x)\]

5.5 Road Conditions

Washboard effect
Wake up strips

5.6 Washboard effect

https://en.wikipedia.org/wiki/Washboarding

Washboarding or corrugation is the formation of periodic, transverse ripples in the surface of gravel and dirt roads.
Washboarding occurs in dry, granular road material with repeated traffic, traveling at speeds above 8.0 kilometres per hour (5 mph).
Washboarding creates an uncomfortable ride for the occupants of traversing vehicles and hazardous driving conditions for vehicles that travel too fast to maintain traction and control.

5.7 Driving on this conditions

5.8 Rumble strip ( wake-up strips)

https://en.wikipedia.org/wiki/Rumble_strip

Rumble strips (also known as sleeper lines or alert strips) are a road safety feature to alert inattentive drivers of potential danger.
The Grooves on the pavement cause a tactile vibration and audible rumbling transmitted through the wheels into the vehicle interior.

5.9 America the beautiful.

5.10 The homogeneous case for damped harmonic oscillator

http://hyperphysics.phy-astr.gsu.edu/hbase/oscda.html

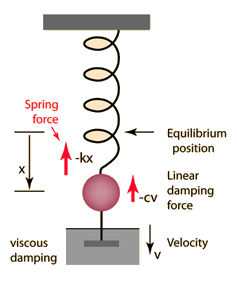
5.11 Solution damped harmonic oscillator

\[m\ddot{x}+c\dot{x}+kx=0\] \[\ddot{x}+\frac{c}{m}\dot{x}+\frac{k}{m}x=0\] \[r^2+\frac{c}{m}r+\frac{k}{m}=0\] \[r_{1,2}=\frac{-\frac{c}{m}\pm\sqrt{\frac{c^2}{m^2}-4\frac{k}{m}}}{2}\]

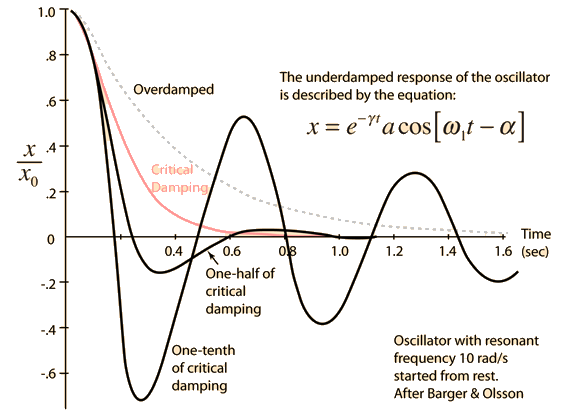
5.12 Three Cases:

Overdamped: \(\frac{c^2}{m^2}>4\frac{k}{m}\) Only real exponentials.
Critical Damping: \(\frac{c^2}{m^2}=4\frac{k}{m}\) a real exponential.
Underdamped: \(\frac{c^2}{m^2}<4\frac{k}{m}\) Real exponential and sinusoidals.

5.13 Plot of the three cases

5.14 2OLNHCC w/o chocks absorvers.

Undamped

\[y''+\omega_0^2y=\frac{F_0}{m}\sin (\omega x), \qquad y(0)=y_0,\quad y'(0)=V_0\] Solution:

STEP 1:

\[r^2+\omega_0^2=0\Rightarrow r_{1,2}=\pm i\omega_0\] \[y_c=c_1\cos(\omega_0 x)+c_2\sin(\omega_0 x)\] i.c.1: \[y_0=c_1\] i.c.2: \[y'=-c_1\omega_0\sin (\omega_0 x)+c_2\omega_0\cos(\omega_0 x)\] \[V_0=c_2\omega_0\rightarrow \boxed{c_2=\frac{V_0}{\omega_0}}\]

\[\boxed{y_c=y_0\cos(\omega_0 x)+\frac{V_0}{\omega_0}\sin(\omega_0 x)}\]

We do know that sin and cosine are similar functions which differ by a phase, then:

\[\cos(\omega_0 x -\phi)=y_0\cos(\omega_0 x)+\frac{V_0}{\omega_0}\sin(\omega_0 x)\]

From trig. we know:

\[\cos (a-b)=\cos(a)\cos(b)+\sin(a)\sin(b)\]

Then \[\cos(\omega_0 x -\phi)=\cos(\omega_0 x)\cos(\phi)+\sin(\omega_0)\sin(\phi) \tag{5.2}\]

Then \[\sin\phi=\frac{V_0}{\omega_0},\qquad\cos\phi=y_0 \tag{5.3}\]

Then \[\tan \phi = \frac{V_0}{\omega_0 y_0}\] And we can find the max amplitude, when \(\cos(\omega_0x-\phi)=1\), that is when argument is zero, that is when \(x=\phi/\omega_0\)

Then Equation 5.2 becomes:

\[\cos(0)=\cos\phi\cos\phi + \sin\phi\sin\phi\] Then using Equation 5.3:

\[\text{Max. Amp.}=\cos^2\phi+\sin^2\phi=y_0^2+\left(\frac{V_0}{\omega_0}\right)^2\]

STEP 2:

\[\frac{F_0}{m}\sin (\omega x)\Rightarrow\]

Then 2 cases:

CASE 1: \(\boxed{\omega\neq\omega_0}\)

\[y_q=\cos(\omega_0 x -\phi)+c_1\cos(\omega x)+c_2\sin(\omega x)\] \[\Rightarrow y_p=c_1\cos(\omega x)+c_2\sin(\omega x)\] \[y'_p=-c_1\omega\sin(\omega x)+c_2\omega\cos(\omega x)\] \[y''_p=-c_1\omega^2\cos(\omega x)-c_2\omega^2\sin(\omega x)\]

\[\Rightarrow\]

\[\begin{align} -c_1\omega^2\cos(\omega x)-c_2\omega^2\sin(\omega x)+&\\ \omega_0^2(c_1\cos(\omega x)+c_2\sin(\omega x))\\ &=\frac{F_0}{m}\sin (\omega x) \end{align}\]

Then I can set my system of equations:

\[-c_2\omega^2+c_2\omega_0^2=\frac{F_0}{m}\] \[-c_1\omega^2+c_1\omega_0^2=0\]

\[\Rightarrow c_1=0\rightarrow c_2=\frac{F_0}{m(\omega_0^2-\omega^2)}\]

\[\Rightarrow \boxed{y=A\cos(\omega_0 x-\phi)+\frac{F_0}{m(\omega_0^2-\omega^2)}\sin(\omega x)}\]

CASE 2: \(\boxed{\omega=\omega_0}\) (Resonance)

\[y_q=\cos(\omega_0 x -\phi)+c_3x\cos(\omega_0 x)+c_4x\sin(\omega_0 x)\] \[\Rightarrow y_p=c_3x\cos(\omega_0 x)+c_4x\sin(\omega_0 x)\]

\[\Rightarrow y_p'=-{c_3} {{\omega}_0} x \sin{\left( {{\omega}_0} x\right) }+{c_4} \sin{\left( {{\omega}_0} x\right) }+{c_4} {{\omega}_0} x \cos{\left( {{\omega}_0} x\right) }+{c_3} \cos{\left( {{\omega}_0} x\right) }\] \[\Rightarrow y_p''=-{c_4} {{{{\omega}_0}}^{2}} x \sin{\left( {{\omega}_0} x\right) }-2 {c_3} {{\omega}_0} \sin{\left( {{\omega}_0} x\right) }-{c_3} {{{{\omega}_0}}^{2}} x \cos{\left( {{\omega}_0} x\right) }+2 {c_4} {{\omega}_0} \cos{\left( {{\omega}_0} x\right) }\]

\[\Rightarrow \]

\[\begin{align} {{{{\omega}_0}}^{2}} \left( {c_4} x \sin{\left( {{\omega}_0} x\right) }+ {c_3} x \cos{\left( {{\omega}_0} x\right) }\right)-&\\ {c_4} {{{{\omega}_0}}^{2}} x \sin{\left( {{\omega}_0} x\right) }-&\\ 2 {c_3} {{\omega}_0} \sin{\left( {{\omega}_0} x\right) }-{c_3} {{{{\omega}_0}}^{2}} x \cos{\left( {{\omega}_0} x\right) }+&\\ 2 {c_4} {{\omega}_0} \cos{\left( {{\omega}_0} x\right) }&\\ &=\frac{F_0}{m}\sin (\omega x) \end{align}\]

Cancelling terms:

\[-2 {{\omega}_0} \left( {c_3} \sin{\left( {{\omega}_0} x\right) }-{c_4} \cos{\left( {{\omega}_0} x\right) }\right) =\frac{F_0}{m}\sin (\omega x)\]

Then \(\boxed{c_4=0}\rightarrow \boxed{c_3=\frac{F_0}{-2m\omega_0}}\)