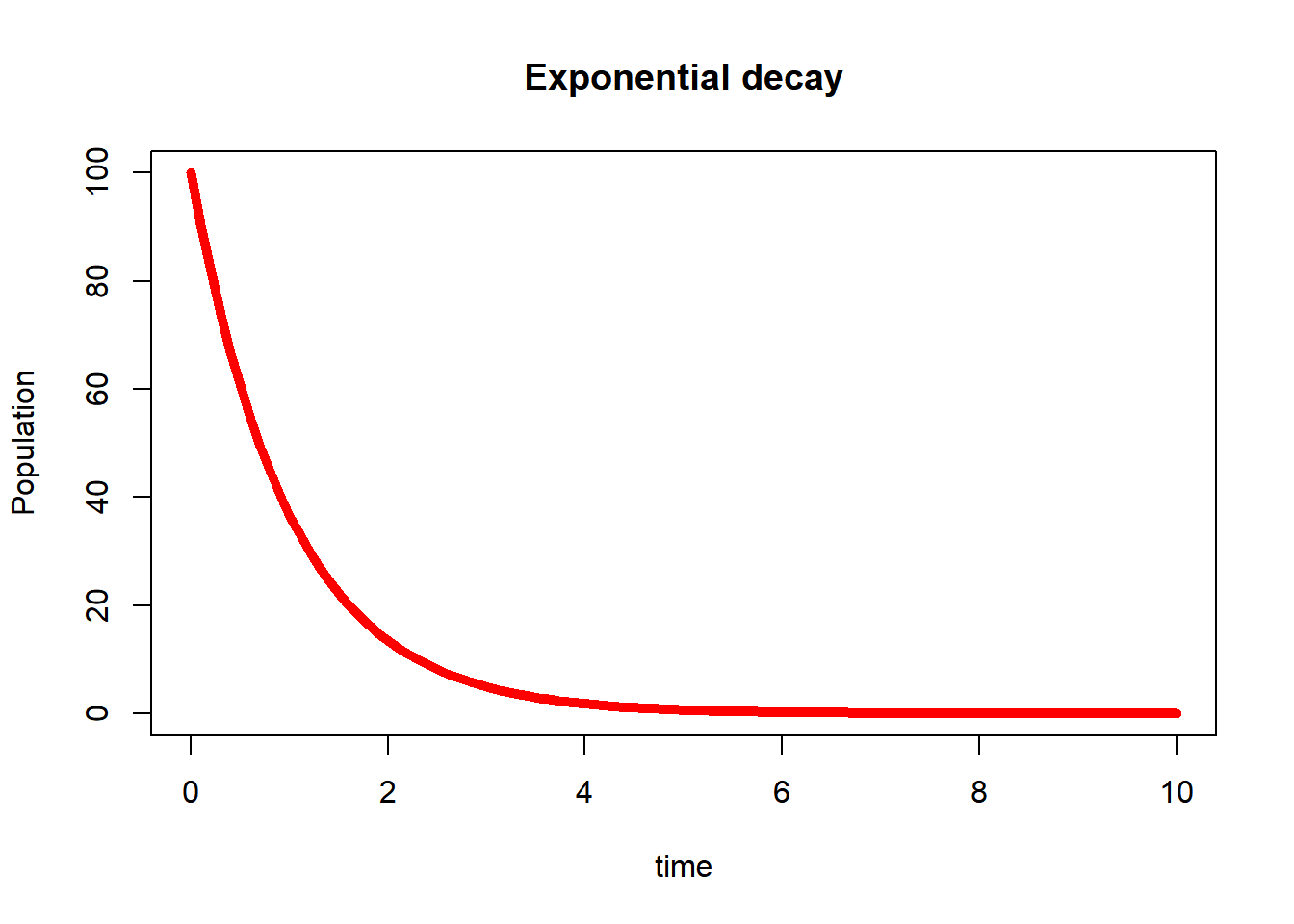
2 L2: First Order diffQ
2.1 Basic Concepts
Note
\[\boxed{N=N_0e^{-kt}}, \quad\text{initial conditions:}\quad N(0)=N_0\] Is a particular solution to the initial value problem:
\[\boxed{\frac{dN}{dt}=-kN},\quad N(0)=N_0,\quad k>0\] - \(N_0\): typically initial population.
- \(k\): decay constant.
2.2 Example: Falling w/o air resistance
Example
A Falling body under the influence of gravity without air resistance.
Solution:
- Newton’s law of gravitation attraction:
\[ F = \frac{Gm_1m_2}{r^2} \]
- Newton’s second law:
\[ F = \frac{d}{dt}(mv) \]
Assumptions: No air resistance, \(h<<R_E\).
Putting all together:
- Now we can solve the diffyQ:
\[\boxed{v=v_0+gt}\]
2.3 Refine Example: Falling with air resistance
Air Resistance
Viscous frictional force (relatively low velocities):
\[F_f=kv \] where \(k\) depends on surface area, viscosity.
Resistive drag force (high velocities):
\[F_d=kv^2 \] where \(k\) depends on surface area, density.
Solution:
- Assumptions: \(h<<R_E\) and viscous friction for air resistance.
\[\begin{align} \sum F &= m\frac{dv}{dt}\\ -kv+mg &=m\frac{dv}{dt}\\ \frac{dv}{dt}&=\frac{mg-kv}{m} \end{align}\]
\[\begin{align} \int \frac{m}{mg-kv}\,dv&=\int dt\\ \text{change of variables}&:(mg-kv=u\rightarrow-kdv=du)\\ \frac{m}{-k}\int \frac{1}{u}\,du &= t+C\\ \ln |u| &= -\frac{k}{m}(t+C)\\ \ln |mg-kv| &= -\frac{k}{m}(t+C) \end{align}\]
\[\begin{align} mg-kv &=e^{-kt/m}\cdot e^C\\ kv &=mg-e^{-kt/m}\cdot e^C \end{align}\]
\[\boxed{v=\frac{1}{k}\left(mg-e^{-kt/m}\cdot e^C\right)}\]
If initial conditions are: \(\boxed{v(0)=0}\) then:
Finally:
\[\boxed{v=\frac{mg}{k}\left(1-e^{-kt/m}\right)}\]
2.4 Terminal velocity:
at terminal velocity: \[t\rightarrow \infty\] \[\Rightarrow\] \[\boxed{v=\frac{mg}{k}\left(1-e^{-kt/m}\right) \rightarrow \frac{mg}{k}(1-0)}\]
\[\boxed{v_{terminal}=\frac{mg}{k}}\]
#| echo: fenced
m <- 100
g <- 10
k <- 20
t <- seq(0, 60, length.out = 100)
v <- m*g/k*(1-exp(-k*t/m))
v_mph <- v * 2.23694
# Adjusting the right margin to create space for the mph label
par(mar=c(5, 4, 4, 4) + 0.1) # Increase the right margin (the fourth value)
# Plot with left axis for velocity in m/s
plot(t, v, type="l", col="red", lwd=5, xlab="time(s)", ylab="velocity(m/s)",
main="Falling with viscous friction of air resistance")
legend("topright", legend= "v=mg/k")
abline(h=m*g/k, col = "blue", lwd=3, lty=2)
# Adding right axis for velocity in mph
par(new=TRUE)
plot(t, v_mph, type="l", col="red", lwd=5, axes=FALSE, xlab="", ylab="", main="")
axis(4)
mtext("velocity (mph)", side=4, line=3) # Label for the right axis2.5 One more math example
Example. u-sustitution
Find the implicit general solution of the differential equation:
\[y^5\frac{dy}{dx}-(y^6+3)\cos x = 0\]
Solution
\[\begin{align} y^5\frac{dy}{dx}&=(y^6+3)\cos x\\ \frac{y^5}{y^6+3}dy&=\cos x\,dx \end{align}\]
\[\begin{align} u=y^6+3&\rightarrow du=6y^5dy\\ \frac{du}{6u}&=\cos x\,dx\\ \frac{1}{6}\ln {|u|}&=\sin x +C\\ \frac{1}{6}\ln {|y^6+3|}&=\sin x +C\\ \frac{\ln {(y^6+3)}}{6}-\sin x &=C \end{align}\]
2.6 After some examples, here the definition
Definition
- A first order differential equation is an equation of the form \(F(t,y,y')=0\)
- A solution of a first order differential equation is a function \(f(t)\) that makes \(F(t,f(t),f′(t))=0\) for every value of \(t\).
2.7 Have questions ?
Schedule Office Hours with your Instructor Here!
2.8 References
- Exponential growth and decay. https://en.wikipedia.org/wiki/Exponential_growth
- Viscous Resistance. http://hyperphysics.phy-astr.gsu.edu/hbase/airfri.html#c3
- First Order Diffq. https://math.libretexts.org/Bookshelves/Calculus/Book%3A_Calculus_(Guichard)/17%3A_Differential_Equations/17.01%3A_First_Order_Differential_Equations
- What is terminal velocity? The Science of Skydiving https://youtu.be/pr78Db9qqeI?feature=shared