4 L4: ODE Separation of Variables (2.1-2.2 part a.)
4.1 ODE Separation of variables (case I)
\[\boxed{\frac{dy}{dx}=f(x)}\]
\[\begin{align} dy&=f(x)\,dx\quad(\text{differential form})\\ \int dy &= \int f(x)\,dx\\ y&=\int f(x)\,dx \end{align}\]
In principle we can integrate the RHS.
A: No. (A lot are though)
4.2 Example
Solve: \[\frac{dy}{dx}=\cos x\]
Sol: \[\begin{align} \int dy &=\int \cos x\, dx\\ y&= \sin x +C \end{align}\]
4.3 ODE Separation of variables (case II)
\[\boxed{\frac{dy}{dx}=f(x,y)}\] We would like to have \(f(x,y)=g(x)h(y)\),
if true, \(\Rightarrow\) \[\begin{align} \frac{dy}{dx}&=g(x)h(y)\\ \frac{1}{h(y)}dy&=g(x)\,dx\quad(\text{Separate variable})\\ \int \frac{1}{h(y)}dy&=\int g(x)\,dx \end{align}\]
Solution may not be valid for all \((x,y)\) values due to singularities.
A: No.
4.4 Definition: Separable
If the \(1^{st}\) order diff. eq\(^n\) can be written in the form \(f(y)\,dy=g(x)\,dx\) it is said to be separable
4.5 Example
Solve: \[\boxed{\frac{dy}{dx}=xy}\]
\[\begin{align} \frac{1}{y}\,dy&=x\,dx,\qquad(y\neq 0)\\ \int\frac{1}{y}\,dy&=\int x\,dx\\ \ln|y|&=\frac{x^2}{2}+C\\ |y|&=e^Ce^{x^2/2},\qquad e^C>0\\ |y|&=De^{x^2/2},\qquad D>0 \end{align}\]
Note: Additional Solution \(y=0\)
A: Maybe (Next time).
4.6 More examples
4.6.1 Example 1:
Solve: \[\frac{dy}{dx}=\frac{2xy}{1+x^2}\]
\[\begin{align} \frac{dy}{dx}&=\frac{2xy}{1+x^2}\\ \frac{1}{y}\,dy&=\frac{2x}{1+x^2}\,dx\\ \int \frac{1}{y}\,dy&=\int \frac{2x}{1+x^2}\,dx\\ \text{(left side trivial,}&\text{right side simple $u$ substitution)}\\ \ln |y| + C_1 &= \int \frac{1}{u}\,du\\ \ln |y| + C_1 &= \ln |u| +C_2\\ \ln |y| &= \ln |1+x^2| +C\\ \text{Let's recall }& C=\ln C_3\\ \Rightarrow\\ \ln |y| &= \ln(1+x^2) +\ln C_3\\ \text{(we know:)}& \qquad(\log (a\cdot b)=\log a+\log b)\\ \Rightarrow\\ \ln |y| &= \ln\left((1+x^2)\cdot \ln C_3\right)\\ |y|&=(1+x^2)\cdot C \end{align}\]
4.6.2 Example 2: Detailed step by step
Solve:
\[\frac{dy}{dx} + 18xy = 0\]
Separate Variables: \[\frac{dy}{y} = -18x \, dx\]
Integrate Both Sides: \[\int \frac{1}{y} \, dy = \int -18x \, dx\]
\[\ln|y| = -9x^2 + C\]
(where \(C\) is the constant of integration)
Solve for \(y\): Taking the exponential of both sides: \[|y| = e^{-9x^2 + C}\]
Since \(|y|\) can be positive or negative, we have two cases:
- Case 1: \(y = e^{-9x^2 + C}\)
- Case 2: \(y = -e^{-9x^2 + C}\)
Simplifying the constant of integration: \[y = \pm e^{-9x^2 + C/2}\]
(where \(C/2\) is another constant)
Therefore, the general solution to the differential equation is:
\[y = A e^{-9x^2} \quad \text{or} \quad y = -A e^{-9x^2}\]
4.6.3 Example 3: Implicit Solutions
Find implicit solutions of \[y'=\frac{2x + 1}{5y^4 + 1},\qquad y(2) = 1\]
\[\begin{align} \frac{dy}{dx}&=\frac{2x + 1}{5y^4 + 1}\\ (5y^4 + 1)\,dy&=(2x+1)\,dx\\ \int (5y^4 + 1)\,dy&=\int (2x+1)\,dx\\ y^5+y+C_1&=x^2+x+C_2,\qquad(\text{absorving})\\ y^5+y&=x^2+x+C \end{align}\]
Now: \(y(2)=1\), then:
\[\begin{align} y^5+y&=x^2+x+C\\ 1^5+1=2^2+2+C\\ \therefore C&= -4\\ \end{align}\]
Finally the implicit solution for the diffyQ with i.c. is:
\[\boxed{y^5+y=x^2+x-4}\]
4.7 More with Khan:
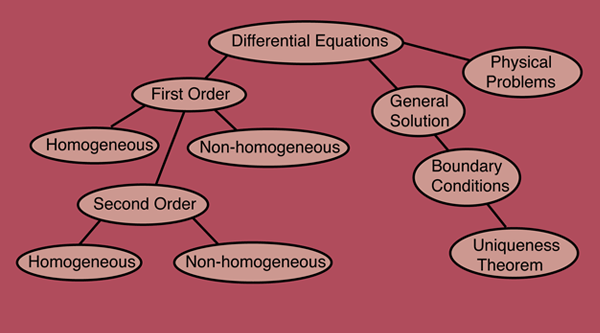
4.8 More with Hyperphysics
4.9 Have questions ?
Schedule Office Hours with your Instructor Here!
4.10 References
- Separation of variables https://en.wikipedia.org/wiki/Separation_of_variables
- More Examples https://www.mathsisfun.com/calculus/separation-variables.html
- Khan diffyQ https://www.khanacademy.org/math/differential-equations
- map. http://hyperphysics.phy-astr.gsu.edu/hbase/de.html#deh
- Quarto revealjs. https://quarto.org/docs/presentations/revealjs/themes.html